선형변환의 합성
회전변환을 하고 전단변환을 한 새로운 선형변환을 보통 앞서 적용한 두 다른 변환의 합성이라 한다
cf. 전단변환 : 직사각형 형태의 영상을 한쪽 방향으로 밀어서 평행사변형 모양으로 변형되는 변환

합성 행렬 (노랑줄 쳐진 행렬)
→ 회전 다음 전단하는 변환의 전체 효과로, 두번의 움직임을 한 번의 동작으로 축약한 것
2x2 행렬의 곱셈
어떤 벡터에 대해 회전변환 후 전단변환을 적용했을 때, 그 전체 결과를 계산하는 방법은
회전변환행렬을 왼쪽에 붙여 벡터에 곱해준 후, 그 왼쪽에 전단변환행렬을 곱해주는 것이다. (회전이 먼저임)
이 계산은 새 합성 행렬과 벡터의 곱셈과 같아야하는데, 새 합성 행렬이 바로 회전 다음 전단한 것이기 때문
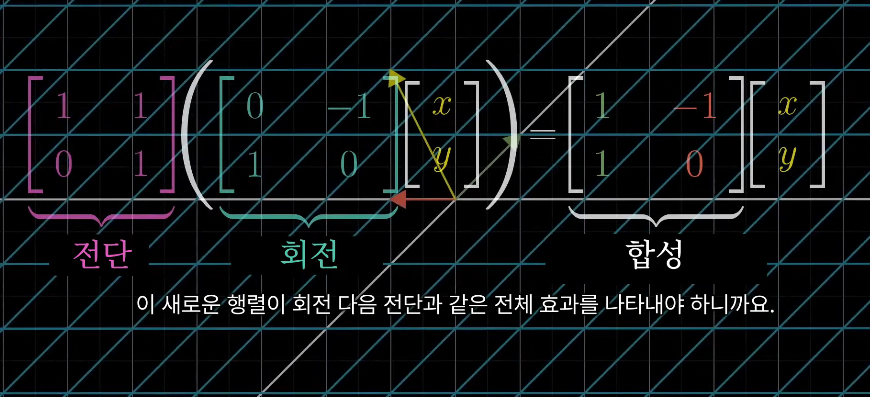
이 식으로 부터 새로운 행렬 (합성 행렬)을 기존 두 행렬의 곱으로 부를 수 있다
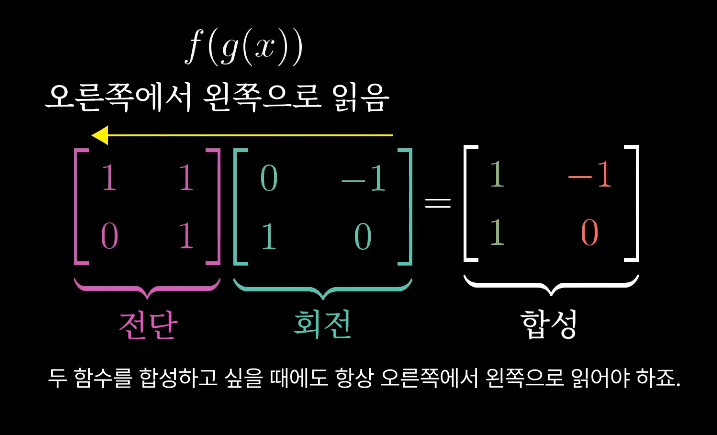
cf. 함수 표기로부터 비롯되기 때문에 오른쪽에서 왼쪽으로 읽음
연산 과정 유도
i^과 j^의 선형변환으로 부터 연산과정을 유도할 수 있다.
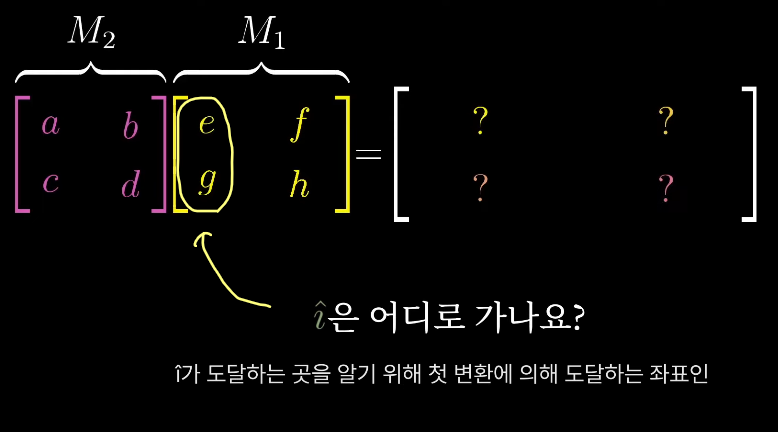
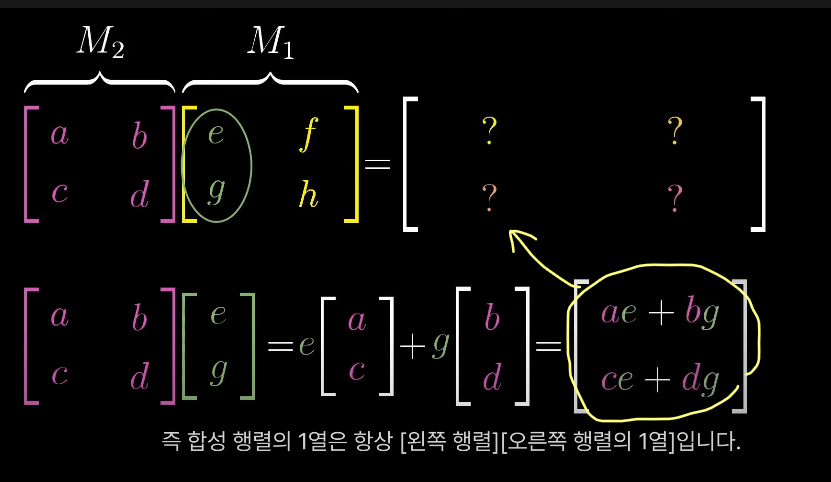
j^도 같은 방식을 거쳐서 아래와 같은 공식이 되는 것
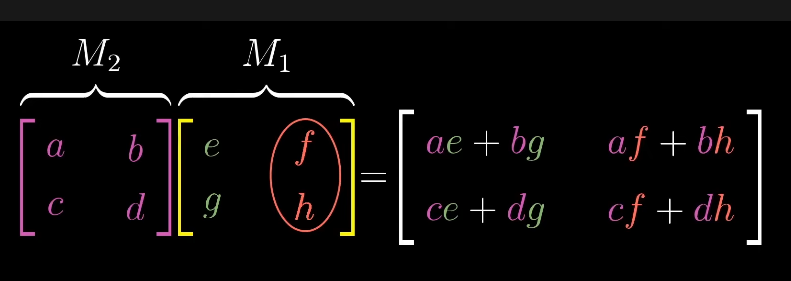
→ 회전 후 전단이라는 점에서 M2와 M1의 위치는 중요하다
why? 회전 후 전단을 하는 것과 전단 후 회전을 하는 것은 다르므 M1 * M2 != M2 * M1
→ 해당 성질로 부터 A(BC) 와 (AB)C 는 같다는 것을 알 수 있다
why? 행렬로 바꿔서 생각하면 오른쪽에서 왼쪽으로 연산되는 것이므로 둘다 C B A 순으로 계산되기 때문
출처
- Essence of Linear Algebra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
선형변환의 합성
회전변환을 하고 전단변환을 한 새로운 선형변환을 보통 앞서 적용한 두 다른 변환의 합성이라 한다
cf. 전단변환 : 직사각형 형태의 영상을 한쪽 방향으로 밀어서 평행사변형 모양으로 변형되는 변환

합성 행렬 (노랑줄 쳐진 행렬)
→ 회전 다음 전단하는 변환의 전체 효과로, 두번의 움직임을 한 번의 동작으로 축약한 것
2x2 행렬의 곱셈
어떤 벡터에 대해 회전변환 후 전단변환을 적용했을 때, 그 전체 결과를 계산하는 방법은
회전변환행렬을 왼쪽에 붙여 벡터에 곱해준 후, 그 왼쪽에 전단변환행렬을 곱해주는 것이다. (회전이 먼저임)
이 계산은 새 합성 행렬과 벡터의 곱셈과 같아야하는데, 새 합성 행렬이 바로 회전 다음 전단한 것이기 때문

이 식으로 부터 새로운 행렬 (합성 행렬)을 기존 두 행렬의 곱으로 부를 수 있다

cf. 함수 표기로부터 비롯되기 때문에 오른쪽에서 왼쪽으로 읽음
연산 과정 유도
i^과 j^의 선형변환으로 부터 연산과정을 유도할 수 있다.


j^도 같은 방식을 거쳐서 아래와 같은 공식이 되는 것
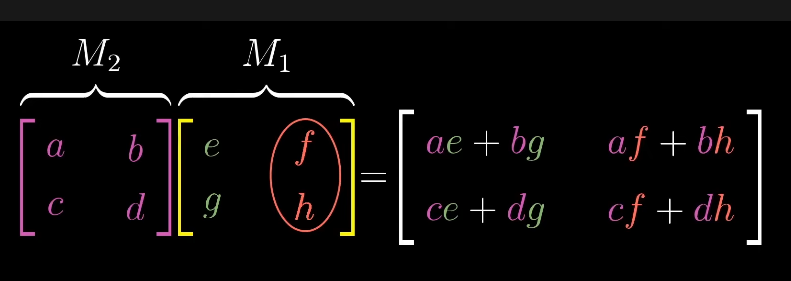
→ 회전 후 전단이라는 점에서 M2와 M1의 위치는 중요하다
why? 회전 후 전단을 하는 것과 전단 후 회전을 하는 것은 다르므 M1 * M2 != M2 * M1
→ 해당 성질로 부터 A(BC) 와 (AB)C 는 같다는 것을 알 수 있다
why? 행렬로 바꿔서 생각하면 오른쪽에서 왼쪽으로 연산되는 것이므로 둘다 C B A 순으로 계산되기 때문
출처
- Essence of Linear Algebra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
