변환의 시각화
변환이란 함수의 다른 말로, 입력이 들어가면 출력을 내놓는 수학적 구조이다
선형대수학에서의 변환은 어떤 벡터를 집어넣을 때 다른 벡터를 내놓는다
그런데 왜 함수라고 쓰지 않고 변환이라 할까?
변환이란 단어는 움직임을 사용한다는 것을 내포한다. (변환을 움직임으로 받아들이자)
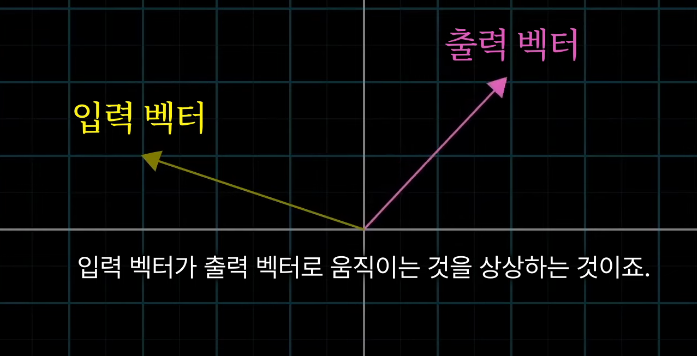

이런 식으로 변환을 생각할 때, 가능한 모든 입출력 벡터 사이의 관계는 공간 내 점이 다른 점으로 움직이는 것으로 나타난다.
선형변환
선형인 변환은 두가지 성질을 갖는다
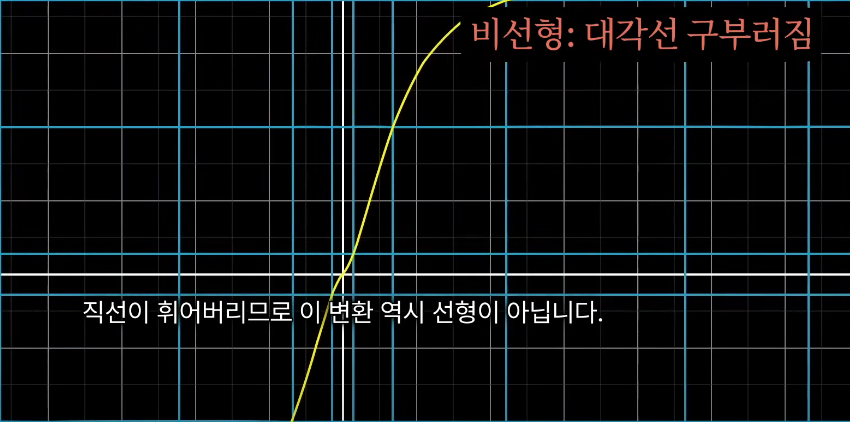
- 모든 직선은 휘지 않고 직선인 상태를 유지
- 원점은 제자리에 고정되어야 함
선형변환을 시각적으로 생각할 때는 격자선이 평행하고 균등한 상태를 유지해야 한다



선형변환은 행렬이다
선형변환들을 (시각적이 아닌) 수치적으로 기술하는 방법은?
일단, 결과적으로 필요한 것은 두 기저벡터 i^, j^ 의 도달점 뿐임
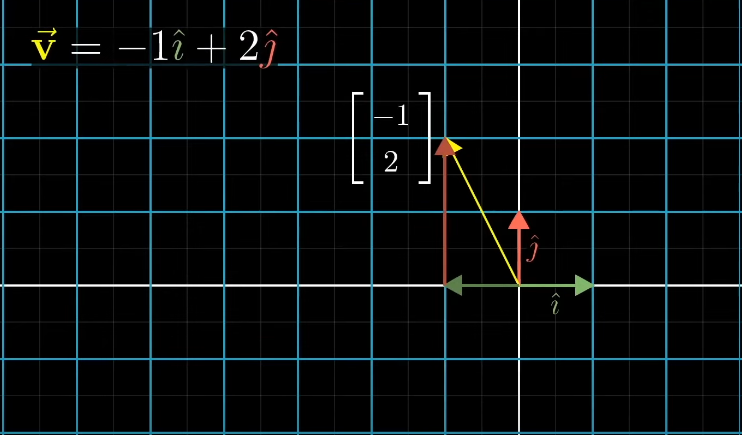


i^과 j^이 움직이는 도달점만 알고있다면 X,Y로 일반화하여 도달 벡터를 알 수 있음
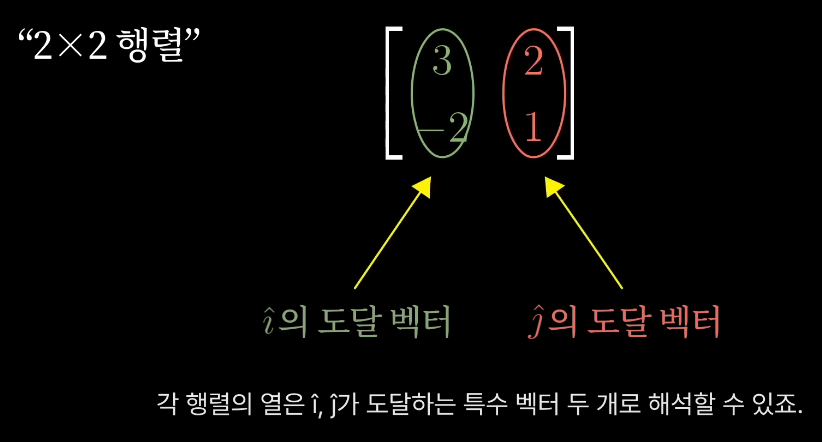
즉, 2차원 선형변환은 두 기저벡터 i^, j^ 의 도달점이라는 숫자 4개로 완벽히 기술될 수 있고 이 i^, j^ 의 도달점은 행렬로 표현가능함
행렬-벡터의 곱셈
행렬은 선형변환을 설명하는 정보를 묶어 표현하는 방법이다

이 공식안에는 열들을 기저벡터의 변환이라고 생각하고, 결과를 그 벡터들의 선형결합으로 생각한다는 의미가 내포되어 있음
요약
- 선형변환은 공간이 움직이는 방식 중 하나로,
격자선이 평행하고 균등한 상태를 유지하면서 원점은 고정되어 있는 것을 만족하는 변환이다 - 선형변환은 숫자 몇 개를 가지고 기술 가능하며 이들은 기저벡터가 도달하는 정보를 포함한다.
- 행렬은 이 변환들을 기술하기 위한 도구이며 각 열이 기저벡터의 도달 좌표이다.
- 행렬-벡터의 곱셈은 변환에 의한 새로운 벡터를 계산하는 방법임
→ 중요한 것은 행렬을 볼 때마다 그것을 일종의 공간 변환으로 해석할 수 있다는 것임
출처
- Essence of Linear Algerbra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
변환의 시각화
변환이란 함수의 다른 말로, 입력이 들어가면 출력을 내놓는 수학적 구조이다
선형대수학에서의 변환은 어떤 벡터를 집어넣을 때 다른 벡터를 내놓는다
그런데 왜 함수라고 쓰지 않고 변환이라 할까?
변환이란 단어는 움직임을 사용한다는 것을 내포한다. (변환을 움직임으로 받아들이자)


이런 식으로 변환을 생각할 때, 가능한 모든 입출력 벡터 사이의 관계는 공간 내 점이 다른 점으로 움직이는 것으로 나타난다.
선형변환
선형인 변환은 두가지 성질을 갖는다
- 모든 직선은 휘지 않고 직선인 상태를 유지
- 원점은 제자리에 고정되어야 함
선형변환을 시각적으로 생각할 때는 격자선이 평행하고 균등한 상태를 유지해야 한다




선형변환은 행렬이다
선형변환들을 (시각적이 아닌) 수치적으로 기술하는 방법은?
일단, 결과적으로 필요한 것은 두 기저벡터 i^, j^ 의 도달점 뿐임



i^과 j^이 움직이는 도달점만 알고있다면 X,Y로 일반화하여 도달 벡터를 알 수 있음
즉, 2차원 선형변환은 두 기저벡터 i^, j^ 의 도달점이라는 숫자 4개로 완벽히 기술될 수 있고 이 i^, j^ 의 도달점은 행렬로 표현가능함

행렬-벡터의 곱셈
행렬은 선형변환을 설명하는 정보를 묶어 표현하는 방법이다

이 공식안에는 열들을 기저벡터의 변환이라고 생각하고, 결과를 그 벡터들의 선형결합으로 생각한다는 의미가 내포되어 있음
요약
- 선형변환은 공간이 움직이는 방식 중 하나로,
격자선이 평행하고 균등한 상태를 유지하면서 원점은 고정되어 있는 것을 만족하는 변환이다 - 선형변환은 숫자 몇 개를 가지고 기술 가능하며 이들은 기저벡터가 도달하는 정보를 포함한다.
- 행렬은 이 변환들을 기술하기 위한 도구이며 각 열이 기저벡터의 도달 좌표이다.
- 행렬-벡터의 곱셈은 변환에 의한 새로운 벡터를 계산하는 방법임
→ 중요한 것은 행렬을 볼 때마다 그것을 일종의 공간 변환으로 해석할 수 있다는 것임
출처
- Essence of Linear Algerbra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
