선형결합
[3,-2]의 각 좌표값을 스칼라로써 생각해본다면, 각 좌표값은 벡터들을 늘리고 줄일 것이다.
xy 좌표계에는 특수한 벡터 두개가 있음
- i^ ( i햇, x-단위벡터) : 오른쪽을 가리키는 길이 1의 벡터
- Ĵ ( j헷, y-단위벡터) : 위쪽을 가리키는 길이 1의 벡터
x좌표를 i햇을 스케일하는 스칼라로, y좌표를 j햇을 스케일하는 스칼라로 생각했을 때,
[3, -2] 좌표쌍이 나타내는 벡터는 두 스케일된 (i햇과 j햇을 스케일) 벡터의 합이다 (벡터를 '스케일된 두 벡터의 합'으로 봄)
여기서 단위 벡터 i햇과 j햇은 특별한 이름을 가지는데, 이 둘을 xy 좌표계의 기저벡터라고 부름 ( i^ , Ĵ : 좌표계의 기저)
→ 즉, [3, -2]에서 스칼라들이 스케일하는 실제 대상들이 바로 이 i햇과 j햇, 즉 기저 벡터이다

여기서 만약 다른 기저벡터를 택했다면, 완전히 새로운 좌표계를 얻을 수 있다는 점이 드러남.

xy 좌표계의 기저 벡터가 아닌 기저벡터를 택하고,
스칼라를 택해 각 벡터를 스케일한 뒤, 두 벡터 더했을 때 얻을 수 있게 될 모든 벡터들에 대해 생각해보자.
여기서 스칼라를 다르게 한다면, 얻을 수 있는 벡터는, 모든 2차원의 벡터이다.

→ 우리가 벡터를 수적으로 표현할 때, 그것은 우리가 암묵적으로 선택한 기저 벡터에 의존하는 것
이처럼 두 벡터를 스케일하고 더하여 새 벡터를 얻는 모든 연산을 두 벡터선형 결합이라 한다

생성 (SPAN)
두 스칼라의 범위를 자유롭게 놓고 얻을 수 있는 모든 가능한 벡터를 고려한다면 3가지 경우가 나온다.
(생성을 위해, 스칼라는 달라지도록 둠)
- 두 가지 벡터의 머리가 다른 곳을 가르킬때 → 즉 대부분의 벡터쌍의 경우, 평면 위 모든 2차원 벡터가 가능함
- 두 기저 벡터가 같은 직선상에 위치한 경우 → 결과 벡터의 끝점이, 원점을 지나는 한 직선으로 제한됨
- 두 벡터가 모두 영벡터인 경우 → 원점에 갇힘



위의 3가지의 경우 처럼,
주어진 벡터 쌍의 선형결합으로 다다를 수 있는 모든 결과벡터의 집합을 '두 벡터의 생성(span)' 이라한다
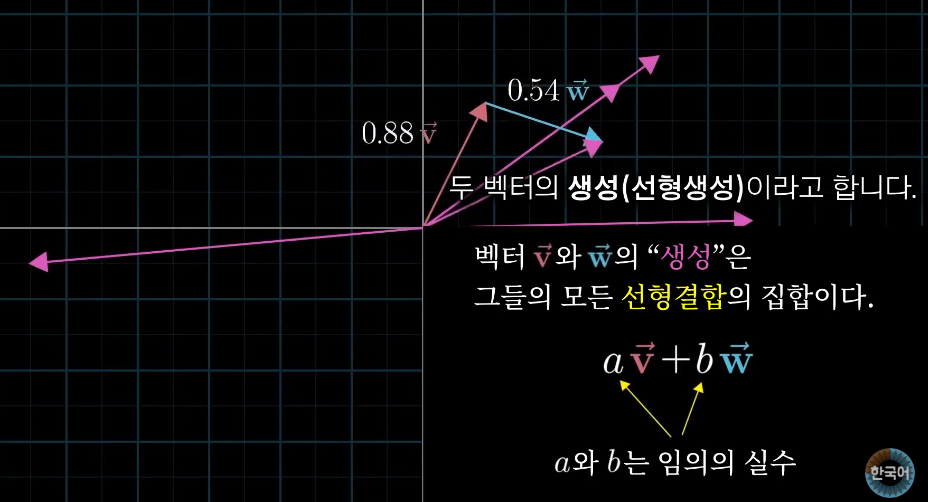
여기서 생성을 표현할 때는, 편의를 위해 점을 사용한다 (벡터의 머리를 점으로, 꼬리는 표현하지 않지만 원점에 있다고 생각)
즉, 일반적으로 벡터 자체를 생각하는 경우에는 화살표로 생각하고 벡터를 모음으로 다루는 경우 점으로 생각한다


3차원 벡터의 생성
3차원 벡터의 생성의 경우 2가지 경우가 있다
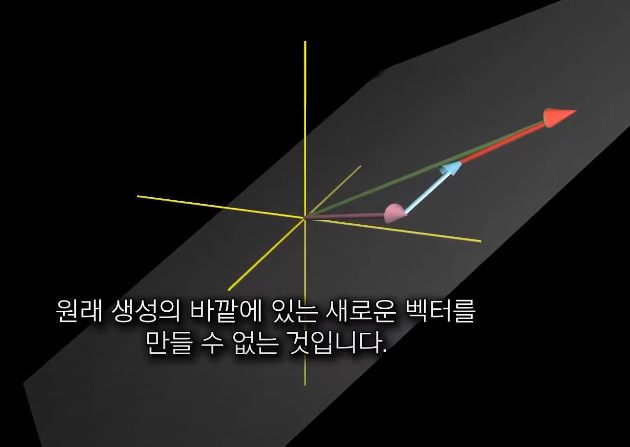
- 세 번째 벡터가 다른 두 벡터의 선형생성에 놓여있다면, 두 벡터와 비교했을 때, 생성은 달라지지 않음 (생성은 똑같이 2차원 평면임)
- 그러나, 세 번째 벡터가 두 벡터의 생성 위에 놓여있지 않는 경우라면, 별개의 방향을 가리키기 때문에 모든 가능한 3차원 벡터에 접근 가능하게 됨



선형종속, 선형독립
2차원 벡터에서 말한, 두 기저 벡터가 같은 직선상에 위치한 경우나
3차원 벡터에서 말한, 하나의 벡터가 다른 두 벡터의 선형생성에 높인 경우는 벡터들 중 최소한 하나는 불필요한 경우다
즉, 생성에 아무것도 더하지 못하는 경우를 '선형종속'이라 한 (벡터 중 하나가 다른 벡터들의 선형결합으로 표현 가능함)


반면, 만약 벡터가 모두가 각자 생성에 다른 차원을 구성한다면 '선형독립'이라 한다.

출처
- Essence of Linear Algebr
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
