2x2 행렬의 행렬식
$ \begin{bmatrix}
3 & 0 \\
0 & 2 \\
\end{bmatrix}$ 행렬을, (1,0) 인 i 햇과 (0,1) 인 j햇을 선형변환한 것이라 생각하면 이 넒이 1*1의 정사각형은 변환 후 2*3인 직사각형이 된다.
영역의 넓이가 원래 1에서 6이 되었으므로, 선형변환은 어떤 넓이를 6배 스케일 했다고 말할 수 있다.
선형변환으로 인해 어떤 스케일 인자만큼 넓이에 변화가 있을 때, 이 인자를 그 변환의 행렬식이라고 한다.

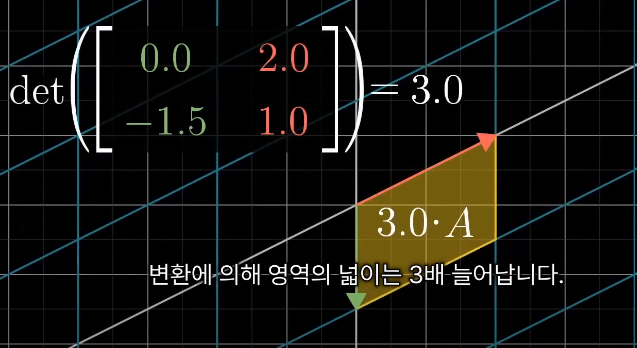
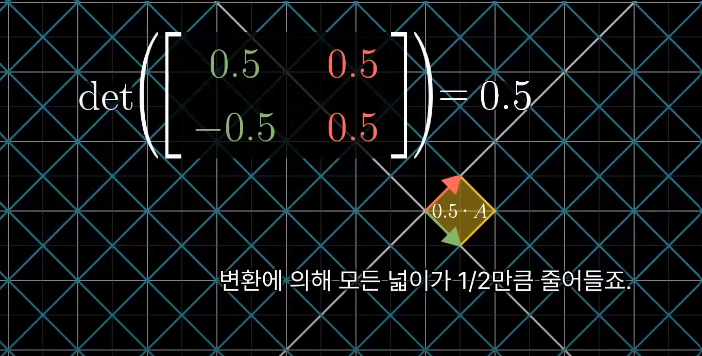
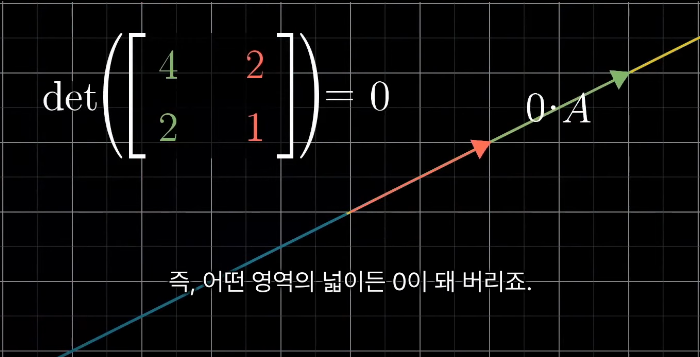
행렬식이 0인 경우는 상당히 중요한데, 행렬의 행렬식이 0인지 확인하면
해당 행렬에 해당하는 변환이, 차원 자체를 낮추는지 여부를 계산할 수 있기 때문이다
음수 행렬식
이전까지의 설명은 양수일 때만 들어맞고, 음수일 때는 또 다른 경우가 생기는데
넓이를 음의 양만큼 스케일한다는 것은 방향과 관련이 있다
(1,0) 인 i햇과 (1,0)인 j햇의 시작 위치는 j햇이 i햇의 왼쪽에 위치한다. 근데 선형변환 후 j햇이 i햇의 오른쪽에 위치한다면
공간의 방향이 뒤집힌 것이고, 방향이 뒤집히는 현상이 일어났을 때의 행렬식이 바로 음수이다
* 단, 이때 행렬식의 절댓값은 여전히 넓이가 스케일된 정도임

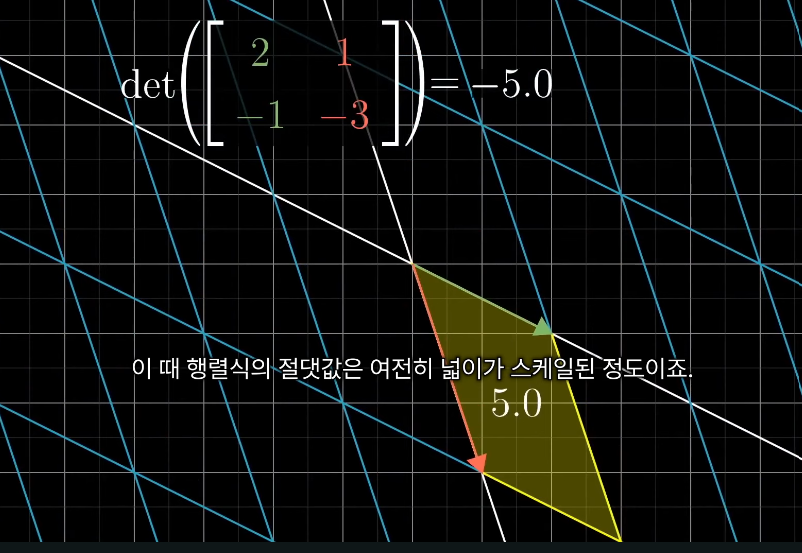
즉, 행렬식이 음수라는 것의 의미는 변환으로 공간이 뒤집히고 넓이는 행렬식만큼 증가한다는 것이다
3x3 행렬의 행렬식
3x3 행렬의 변환도 얼마나 스케일하느냐에 관한 것인데, 해당 행렬에서는 부피를 얼마나 스케일하느냐이다.
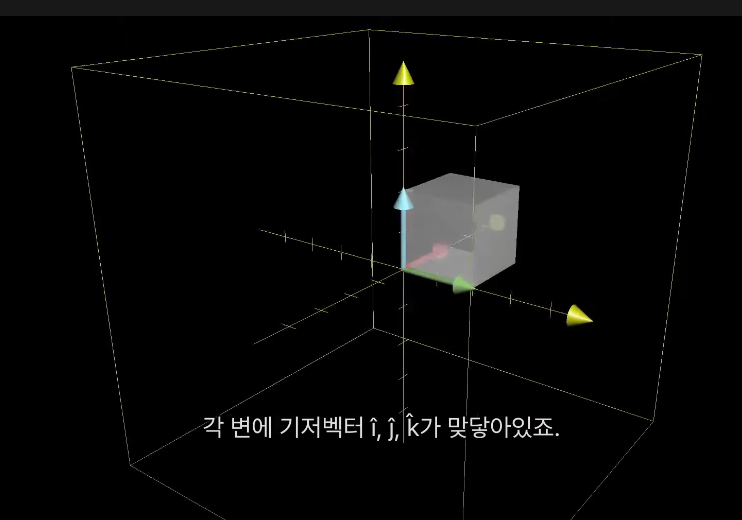
1x1x1 의 정육면체는 변환 후, 기울어질 대로 기울어진 평행 육면체가 되는데
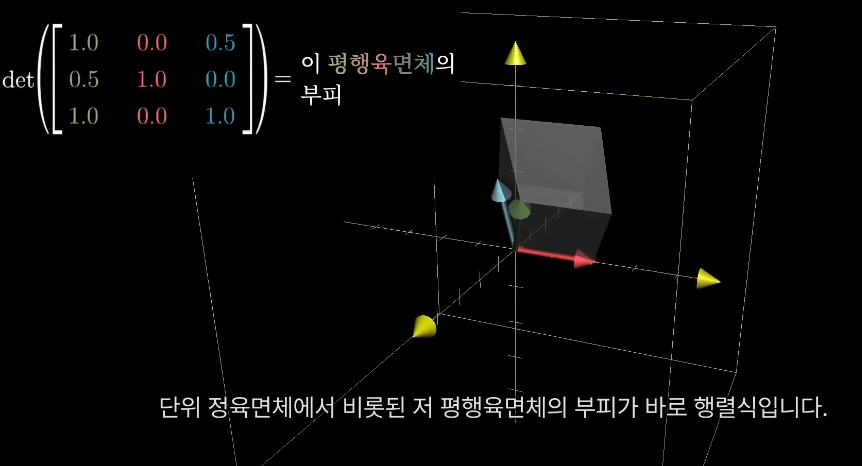
행렬식은 부피의 스케일 인자를 주기 떄문에 3x3 행렬의 행렬식은 평행육면체의 부피가 된다.
행렬식이 0
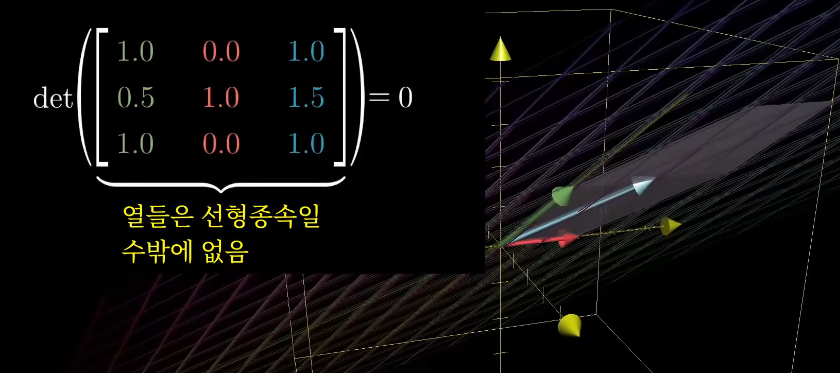
만약 행렬식이 0이면 공간의 전체가 부피가 0인 평면, 직선, 점 등 무언가로 변하는데 그 경우, 행렬의 각 열들은 선형종속일 수 박에 없다 (2장 참고)
행렬식이 음수
3차원에서 방향을 기술할 때는 오른손 법칙을 사용한다
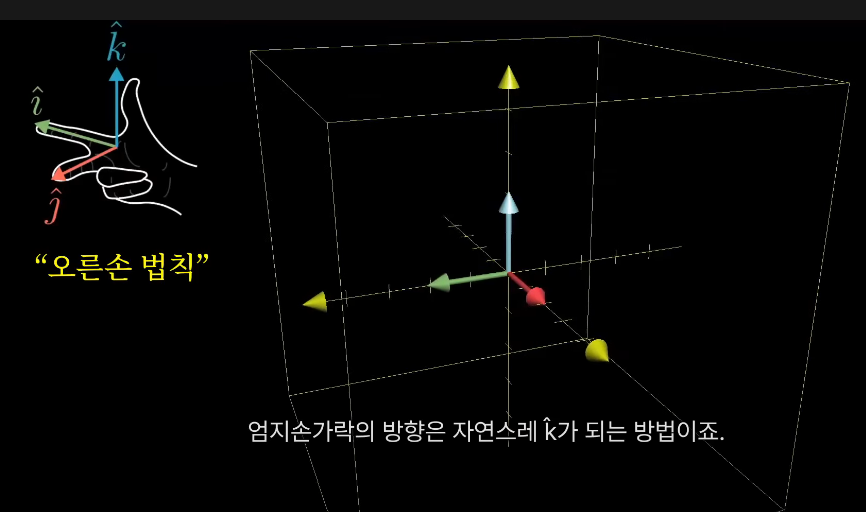
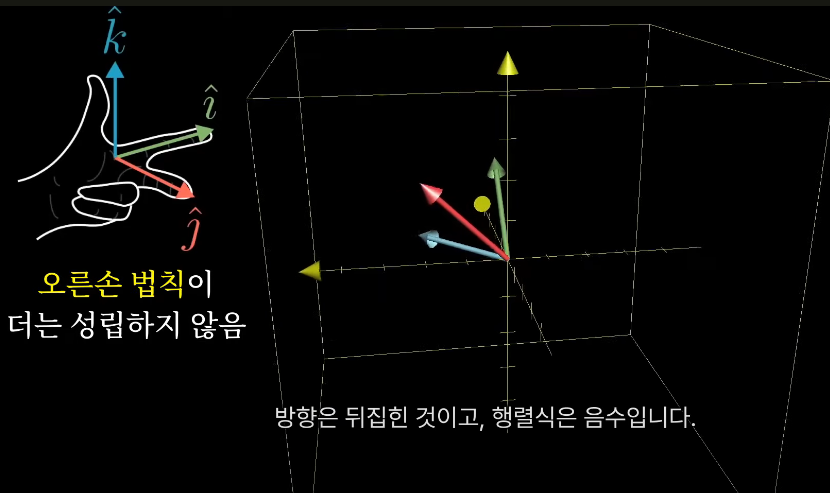
변환 후에도 법칙이 오른손에서 성립하면 방향은 뒤집히지 않은 것이며, 행렬식은 양수이다
만약, 변환 후 법칙이 왼손에서 성립하면 방향은 뒤바뀐 것이고, 행렬식은 음수이다
행렬식 계산


직관은 강의를 통해서,,, 어렵다,,
중요한 것은 계산식이 아니라, 행렬식이 무엇을 나타내는지를 이해하는 것이다!
출처
- Essence of Linear Algebra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
2x2 행렬의 행렬식
$ \begin{bmatrix}
3 & 0 \\
0 & 2 \\
\end{bmatrix}$ 행렬을, (1,0) 인 i 햇과 (0,1) 인 j햇을 선형변환한 것이라 생각하면 이 넒이 1*1의 정사각형은 변환 후 2*3인 직사각형이 된다.
영역의 넓이가 원래 1에서 6이 되었으므로, 선형변환은 어떤 넓이를 6배 스케일 했다고 말할 수 있다.
선형변환으로 인해 어떤 스케일 인자만큼 넓이에 변화가 있을 때, 이 인자를 그 변환의 행렬식이라고 한다.




행렬식이 0인 경우는 상당히 중요한데, 행렬의 행렬식이 0인지 확인하면
해당 행렬에 해당하는 변환이, 차원 자체를 낮추는지 여부를 계산할 수 있기 때문이다
음수 행렬식
이전까지의 설명은 양수일 때만 들어맞고, 음수일 때는 또 다른 경우가 생기는데
넓이를 음의 양만큼 스케일한다는 것은 방향과 관련이 있다
(1,0) 인 i햇과 (1,0)인 j햇의 시작 위치는 j햇이 i햇의 왼쪽에 위치한다. 근데 선형변환 후 j햇이 i햇의 오른쪽에 위치한다면
공간의 방향이 뒤집힌 것이고, 방향이 뒤집히는 현상이 일어났을 때의 행렬식이 바로 음수이다
* 단, 이때 행렬식의 절댓값은 여전히 넓이가 스케일된 정도임


즉, 행렬식이 음수라는 것의 의미는 변환으로 공간이 뒤집히고 넓이는 행렬식만큼 증가한다는 것이다
3x3 행렬의 행렬식
3x3 행렬의 변환도 얼마나 스케일하느냐에 관한 것인데, 해당 행렬에서는 부피를 얼마나 스케일하느냐이다.
1x1x1 의 정육면체는 변환 후, 기울어질 대로 기울어진 평행 육면체가 되는데
행렬식은 부피의 스케일 인자를 주기 떄문에 3x3 행렬의 행렬식은 평행육면체의 부피가 된다.


행렬식이 0
만약 행렬식이 0이면 공간의 전체가 부피가 0인 평면, 직선, 점 등 무언가로 변하는데 그 경우, 행렬의 각 열들은 선형종속일 수 박에 없다 (2장 참고)

행렬식이 음수
3차원에서 방향을 기술할 때는 오른손 법칙을 사용한다


변환 후에도 법칙이 오른손에서 성립하면 방향은 뒤집히지 않은 것이며, 행렬식은 양수이다
만약, 변환 후 법칙이 왼손에서 성립하면 방향은 뒤바뀐 것이고, 행렬식은 음수이다
행렬식 계산


직관은 강의를 통해서,,, 어렵다,,
중요한 것은 계산식이 아니라, 행렬식이 무엇을 나타내는지를 이해하는 것이다!
출처
- Essence of Linear Algebra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
