벡터를 바라보는 3가지 관점
벡터를 바라보는 관점에는 서로 다르지만 관련된 3가지로 물리학자, 컴퓨터 과학자, 수학자의 관점이 존재한다.
- 물리학자의 벡터 : 공간 상의 한 화살표. 벡터의 길이와 방향이 같다면 어디에 옮겨도 같은 벡터
- 컴퓨터 과학자의 벡터 : 숫자 자료를 배열한 것 (벡터 = 숫자의 나열)
: 2차원 벡터란 말은 단지 숫자가 두줄로 배열됐음을 의미 (단, 숫자 위치 중요) - 수학자의 벡터 : 덧셈과 상수배를 포함해 다른 연산들이 성립할 수만 있다면 뭐든 벡터임
해당 관점은 그렇구나~ 정도로만 하면되고, 중요한 것은 선형대수학 내에서는 벡터의 덧셈과 상수배가 중요하다는 것
시리즈 속 벡터의 시각화
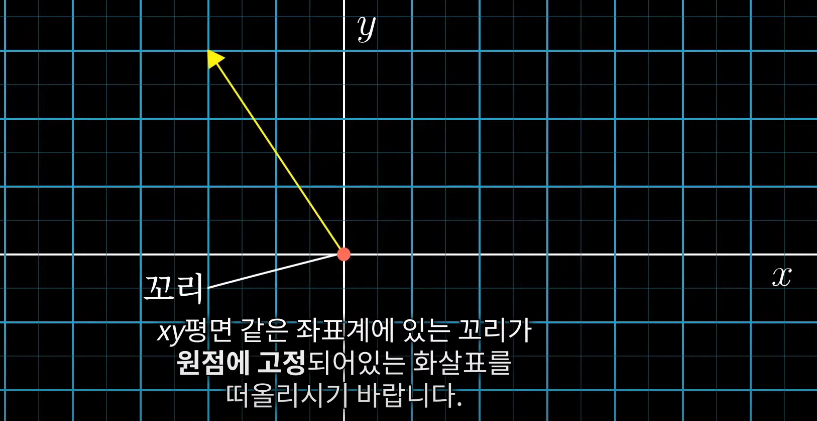
벡터의 시각화
화살표가 떠올라야함. 특히, 꼬리가 원점에 고정되어 있는 화살표
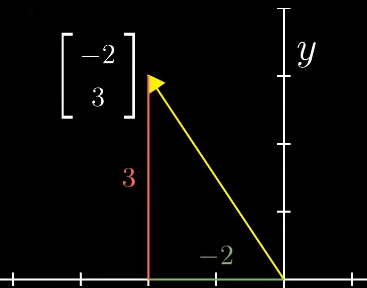
벡터의 좌표
벡터의 좌표는 한 쌍의 숫자이며, 이들은 기본적으로 벡터의 머리가 꼬리(원점)로부터 얼마나 떨어져 있느냐를 나타냄
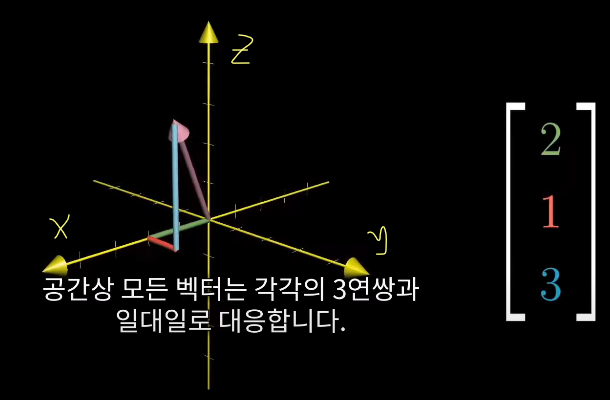
모든 숫자 쌍과 모든 벡터는 각각에 대해 일대일로 대응한다 (첫번째 - x축, 두번째 - y축, 세번째 - z축)
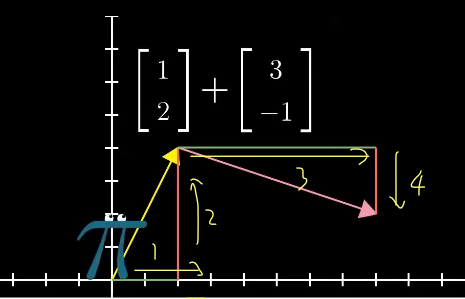
벡터의 덧셈
벡터 w를 움직여, 꼬리를 벡터 v의 머리에 오도록 놓고, 원점으로 부터 w의 머리를 연결한 새로운 벡터가 v, w의 합
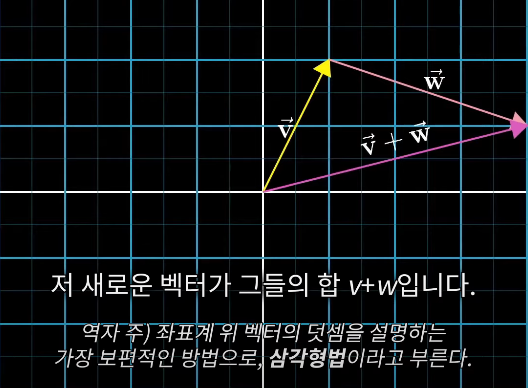
삼각형법으로 벡터를 더할 때, 더해주는 벡터 w의 꼬리는 벡터 v의 머리에 온다
→ 수직선위의 숫자를 더하는 과정의 확장이 됨 (수평끼리 더하고, 수직끼리 더한다)
벡터의 상수배
상수합을 곱해주면 그 값에 따라 벡터가 늘어나고, 줄어들고, 뒤집힘
→ 양수 곱 : 양수 만큼 늘어남 / 분수 곱 : 분수만큼 줄어듦 / 음수 곱 : 음수 만큼 뒤집혀서 늘어남
이처럼, 벡터의 방향은 유지한 채 그 길이를 늘이고 줄이고 뒤집는 등의 과정을 '스케일' 한다고 하며,
벡터를 스케일하는 숫자를 스칼라라고 한다.
즉, 주어진 벡터의 상수배 (스칼라배)란 각 항에 그 스칼라를 곱하는 것을 의미함
선형대수학의 용도
선형대수학의 용도는 어떤 대상 사이의 상호작용을 해석하는 능력을 다루는 것임
데이터 분석가에게 선형대수학은 많은 숫자의 배열을 시각적으로 개념화하기 좋은 방법을 제공한다.
데이터 속 패턴을 설명하고, 어떤 연산들에 관한 보편적인 관점을 제공함
출처
- Essence of Linear Algebra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
해당 강의를 보고, 이제껏 선형대수학을 단순 수적 연산으로만 접근했구나 싶었다.
수 이전에 기하학적인 이해를 먼저하는 것의 중요성을 알려주는 강의
