연립선형방정식의 기하적 해석
지수가 붙거나, 변수끼리 곱해져 있지 않고 단지 스케일되어 있는 각 변수가 더해져 있기만 한 연립선형방정식은 행렬-벡터의 곱셈의 형태와 유사하다
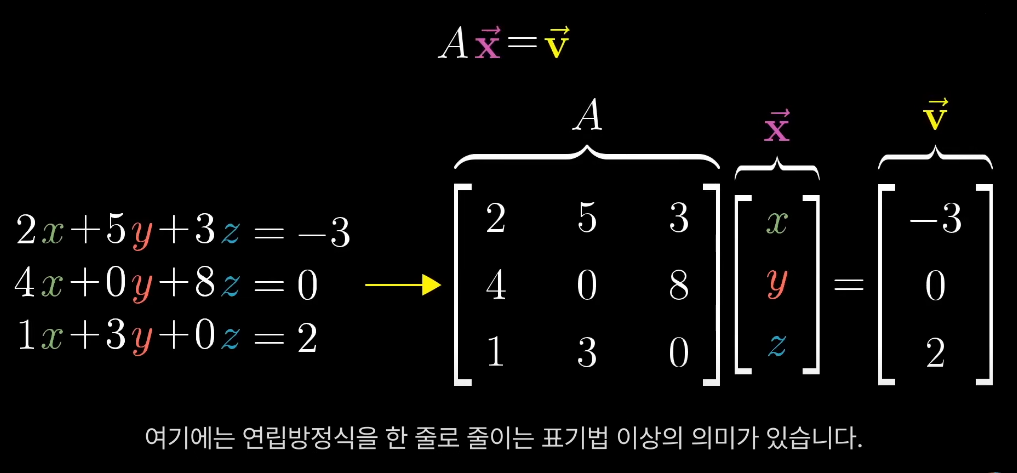
해당 표기법으로 기하적 해석에 접근해볼 수 있다
행렬은 어떤 선형변환에 대응되기 때문에 방정식 Ax = v를 푸는 것은 변환 후 v가 되는 벡터 x를 구하는 것이다
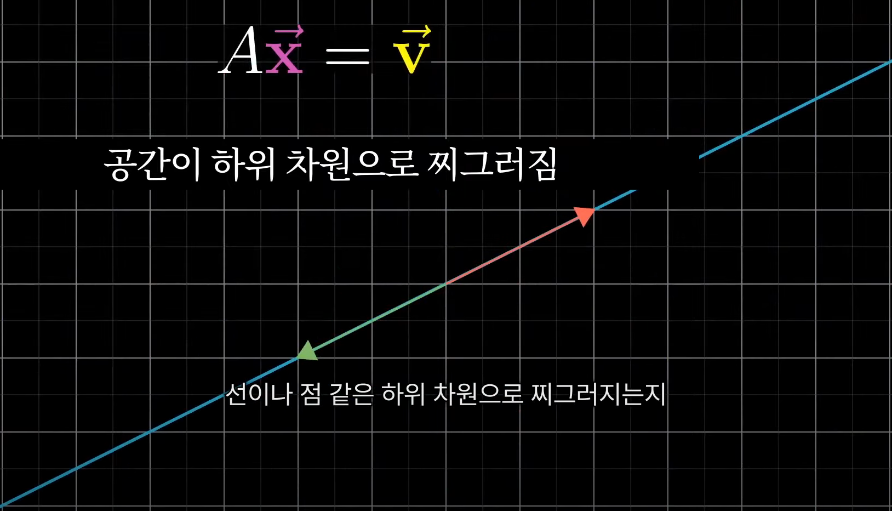
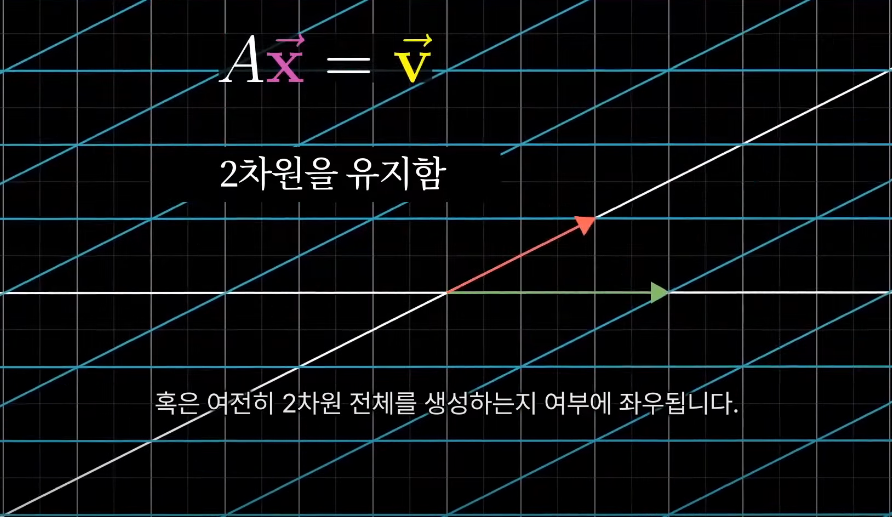
방정식의 해를 생각하는 방법은, 변환으로 인해 공간 전체가 선이나 점 같은 하위차원으로 찌그러지는지 혹은, 여전히 2차원 전체를 생성하는지 여부에 좌우되는데,
이는 행렬식이 0인지, 0이 아닌지 여부에 좌우된다는 것과 같다 (6강 참고)
역행렬; 0이 아닌 행렬식 (det(A) != 0)
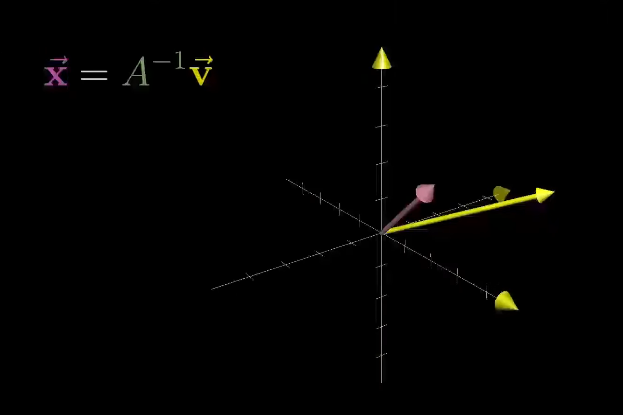
해당 경우, v에 도달하는 단 하나의 벡터가 존재하며 그 벡터는 변환을 거꾸로 돌리면 찾을 수 있다
변환을 거꾸로 돌린다는 것은 별개의 선형 변환을 적용하는 것과 같고 보통 이를 \(A\)의 역이라 하며 \(A^{-1}\)로 표기한다

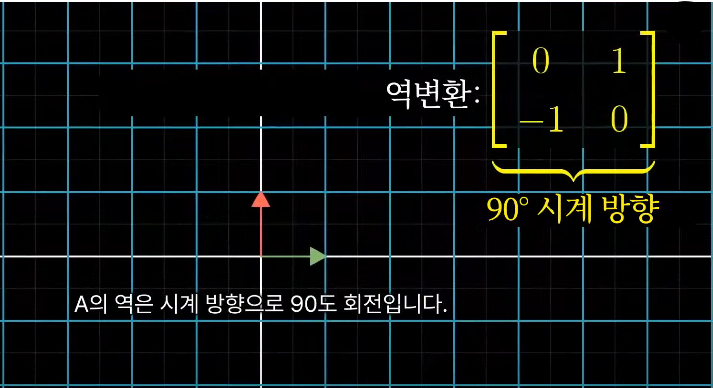
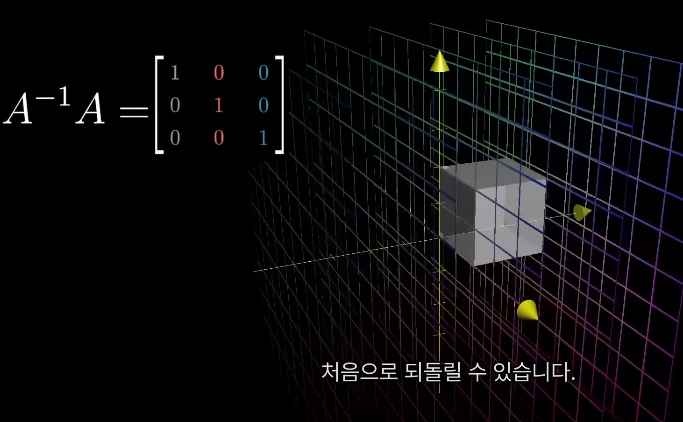
\(A^{-1}\)를 유일하게 정의하는 성질은 \(A\)*\(A^{-1}\) 하면 처음으로 돌아온다는 것이다 ( = \(A\)*\(A^{-1}\) 가 아무것도 안 하는 변환과 같다)
아무 것도 하지 않는 변환은 항등변환이라고 한다. 또한, i^과 j^이 자리에서 움직이지 않으니 행렬로는 [1 0; 0 1]이 된다
즉, 행렬식이 0 이 아닌 이상 항상 \(A^{-1}\)은 존재하여 A를 적용한 다음, \(A^{-1}\)를 적용하면 처음으로 되돌릴 수 있다.
이로 방정식을 풀 때는 그냥 벡터 v에 역행렬을 곱하면 된다.


행렬식이 0인 경우 (det(A) = 0)
위와 다르게, 행렬식이 0이라 방정식계와 연관된 변환이 공간을 하위 차원으로 찌그러뜨리는 경우는 역이 존재하지 않는다
즉, 부피가 0인 영역으로 찌그러지면 행렬식이 0인 경우임
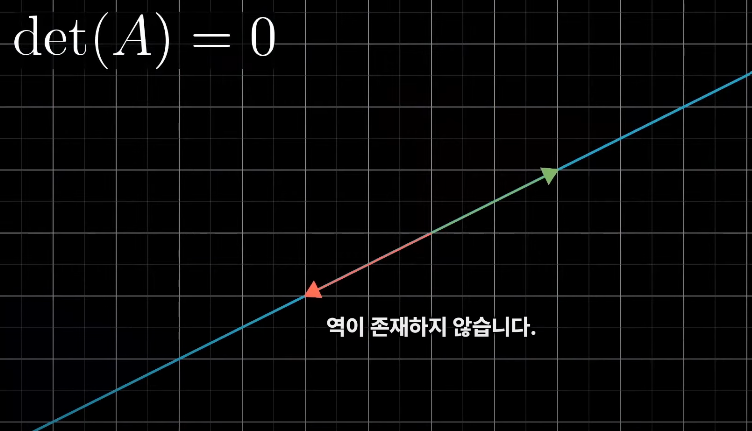
* det(A) = 0인 경우 역이 존재하지 않는거지 해는 존재할 수 있음
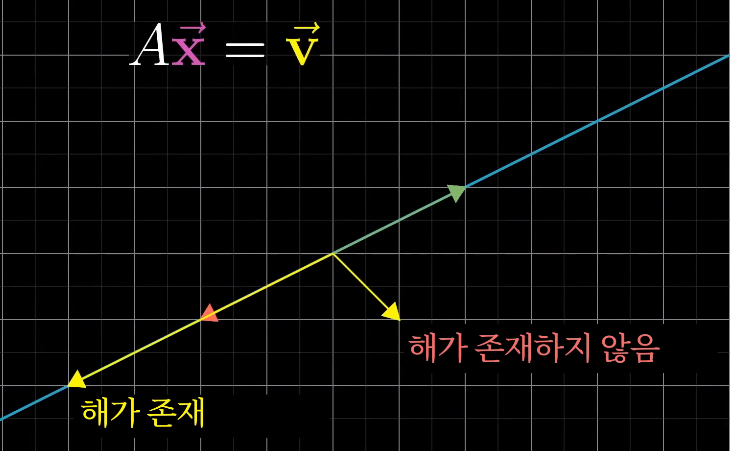
랭크, 열공간
랭크 (차수, 계수)
똑같이 행렬식이 0인 경우여도 어떤 경우는 해가 훨씬 더 제한적으로 존재하는데,
이럴때 행렬식이 0이란 말보다 더 구체적인 표현이 필요하고 그것이 랭크 (차수, 계수)이다
- 변환 후 출력이 직선, 즉 1차원일 때는 변환의 랭크가 1
- 모든 벡터가 어떤 2차원 평면 위에 있다면, 변환의 랭크가 2
→ 즉 랭크는 변환 후 출력의 차원 수를 말한다
따라서, 2*2 행렬은 가능한 최대 랭크가 2이고, 3*3 행렬은 가능한 최대 랭크가 3이다.
만약, 3*3 행렬이 랭크가 2라면 공간이 붕괴된 경우임
열공간
선, 평면, 3차원 공간처럼 행렬에 대해 가능한 모든 출력의 집합을 행렬의 열공간이라 한다.
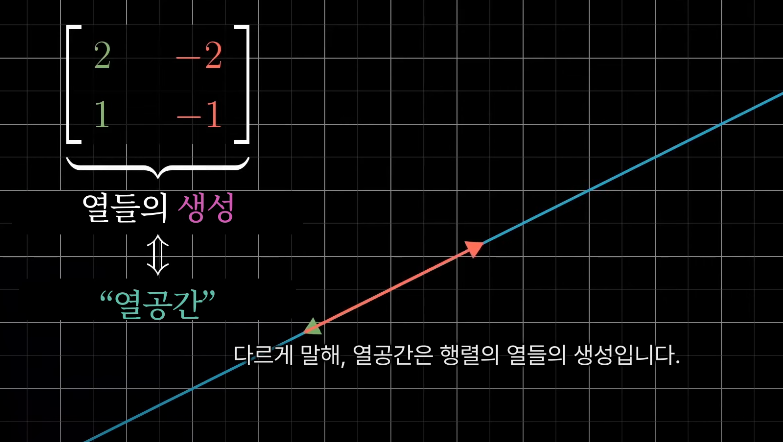
→ 따라서, 랭크의 더 정확한 정의는 열공간의 차원수
영공간
랭크가 최대인 경우, 즉 랭크가 행렬의 열 수와 같으면 풀 랭크(full-rank)라 한다 (= 공간이 찌그러지지 않음)
풀랭크일 때, 원점에 도달하는 벡터는 0 자신 뿐이다

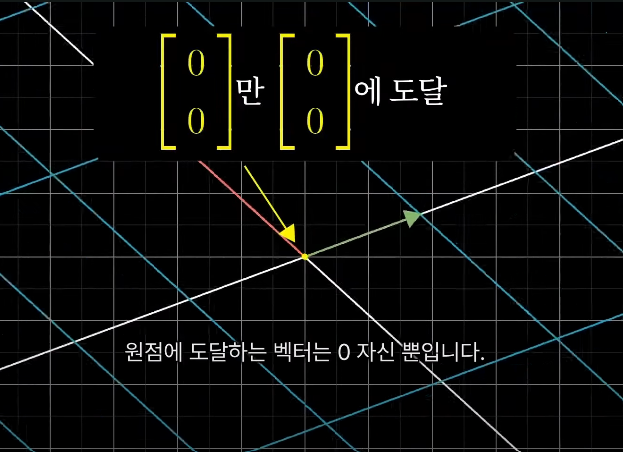
하지만, 풀 랭크가 아닌 변환에 의해 공간이 하위 차원으로 찌그러지면 0에 도달하는 벡터가 한뭉치 생김
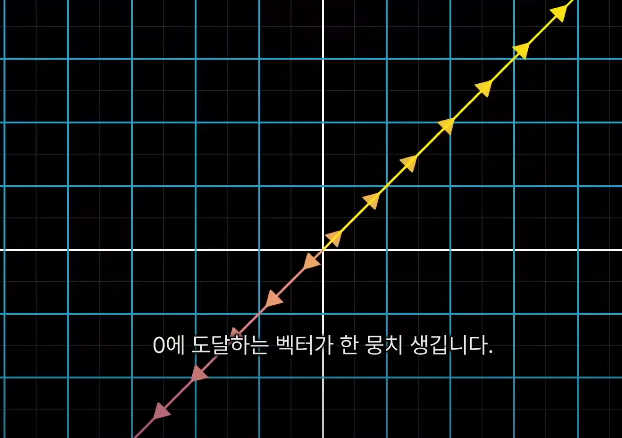
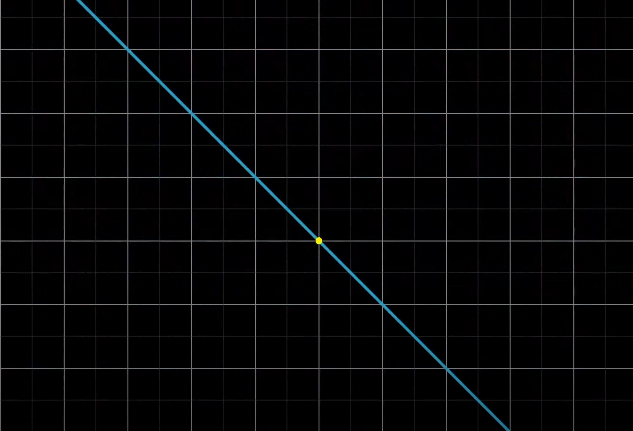
이처럼 원점에 도달하는 벡터의 집합을 영공간 또는 핵이라고 함
즉 영공간은 null이 되는, 영벡터에 도달하는 모든 벡터의 공간을 뜻하는 것
이를 연립방정식으로 생각해보면 Ax = [0,0] 이고 영공간은 방정식의 가능한 모든 해가 된다
출처
- Essence of Linear Algebra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
연립선형방정식의 기하적 해석
지수가 붙거나, 변수끼리 곱해져 있지 않고 단지 스케일되어 있는 각 변수가 더해져 있기만 한 연립선형방정식은 행렬-벡터의 곱셈의 형태와 유사하다

해당 표기법으로 기하적 해석에 접근해볼 수 있다
행렬은 어떤 선형변환에 대응되기 때문에 방정식 Ax = v를 푸는 것은 변환 후 v가 되는 벡터 x를 구하는 것이다
방정식의 해를 생각하는 방법은, 변환으로 인해 공간 전체가 선이나 점 같은 하위차원으로 찌그러지는지 혹은, 여전히 2차원 전체를 생성하는지 여부에 좌우되는데,
이는 행렬식이 0인지, 0이 아닌지 여부에 좌우된다는 것과 같다 (6강 참고)


역행렬; 0이 아닌 행렬식 (det(A) != 0)
해당 경우, v에 도달하는 단 하나의 벡터가 존재하며 그 벡터는 변환을 거꾸로 돌리면 찾을 수 있다
변환을 거꾸로 돌린다는 것은 별개의 선형 변환을 적용하는 것과 같고 보통 이를 \(A\)의 역이라 하며 \(A^{-1}\)로 표기한다


\(A^{-1}\)를 유일하게 정의하는 성질은 \(A\)*\(A^{-1}\) 하면 처음으로 돌아온다는 것이다 ( = \(A\)*\(A^{-1}\) 가 아무것도 안 하는 변환과 같다)
아무 것도 하지 않는 변환은 항등변환이라고 한다. 또한, i^과 j^이 자리에서 움직이지 않으니 행렬로는 [1 0; 0 1]이 된다
즉, 행렬식이 0 이 아닌 이상 항상 \(A^{-1}\)은 존재하여 A를 적용한 다음, \(A^{-1}\)를 적용하면 처음으로 되돌릴 수 있다.
이로 방정식을 풀 때는 그냥 벡터 v에 역행렬을 곱하면 된다.




행렬식이 0인 경우 (det(A) = 0)
위와 다르게, 행렬식이 0이라 방정식계와 연관된 변환이 공간을 하위 차원으로 찌그러뜨리는 경우는 역이 존재하지 않는다
즉, 부피가 0인 영역으로 찌그러지면 행렬식이 0인 경우임

* det(A) = 0인 경우 역이 존재하지 않는거지 해는 존재할 수 있음

랭크, 열공간
랭크 (차수, 계수)
똑같이 행렬식이 0인 경우여도 어떤 경우는 해가 훨씬 더 제한적으로 존재하는데,
이럴때 행렬식이 0이란 말보다 더 구체적인 표현이 필요하고 그것이 랭크 (차수, 계수)이다
- 변환 후 출력이 직선, 즉 1차원일 때는 변환의 랭크가 1
- 모든 벡터가 어떤 2차원 평면 위에 있다면, 변환의 랭크가 2
→ 즉 랭크는 변환 후 출력의 차원 수를 말한다
따라서, 2*2 행렬은 가능한 최대 랭크가 2이고, 3*3 행렬은 가능한 최대 랭크가 3이다.
만약, 3*3 행렬이 랭크가 2라면 공간이 붕괴된 경우임
열공간
선, 평면, 3차원 공간처럼 행렬에 대해 가능한 모든 출력의 집합을 행렬의 열공간이라 한다.

→ 따라서, 랭크의 더 정확한 정의는 열공간의 차원수
영공간
랭크가 최대인 경우, 즉 랭크가 행렬의 열 수와 같으면 풀 랭크(full-rank)라 한다 (= 공간이 찌그러지지 않음)
풀랭크일 때, 원점에 도달하는 벡터는 0 자신 뿐이다


하지만, 풀 랭크가 아닌 변환에 의해 공간이 하위 차원으로 찌그러지면 0에 도달하는 벡터가 한뭉치 생김


이처럼 원점에 도달하는 벡터의 집합을 영공간 또는 핵이라고 함
즉 영공간은 null이 되는, 영벡터에 도달하는 모든 벡터의 공간을 뜻하는 것
이를 연립방정식으로 생각해보면 Ax = [0,0] 이고 영공간은 방정식의 가능한 모든 해가 된다
출처
- Essence of Linear Algebra
선형대수학의 본질 | 3b1b 한국어
3Blue1Brown의 대표 시리즈 "Essence of Linear Algebra"의 한국어 번역. 행렬, 행렬식, 고윳값-고유벡터 등에 관한 기하적 직관을 선보임으로써 선형대수학의 이해를 돕습니다.
www.youtube.com
