t-test를 이해하는 데 앞서, 정규분포, 표준정규분포, z-test 다음으로 이해해야하는 것이 양측검정, 단측검정이다.
앞선 키 예제를 그대로 사용함!
양측검정 vs 단측검정

* D = 차이 / Da-b : A와 B의 차
대립가설에서 양측검정은 의미상 크거나 작다를 모두 포함한 경우이고, 단측검정은 둘 중 하나만을 채택한 경우이다.
양측검정과 단측검정의 사용에 있어, 정해진 것이 없기 떄문에 연구자의 판단에 따라 사용하면 된다.
( 보통 단측이 한가지 경우만을 대립가설로 가져가기 때문에, 연구자가 설립한 가설을 확신할 수 있을 떄 단측을 사용하는 경우가 많음)
앞선 포스팅에서 1.4cm란 키차이가 우연히 발생했을 확률은 얼마나 될까? 했을 때,
확률이 유의수준 0.05보다 작으면 우연이 아니라고 보고, 0.05보다 크면 우연이라고 본다고 했다.
이에, 우연이다라는 확률을 보기 위한 것이기 때문에 확률 곡선을 가지고 판단을 해야한다.

* 우연이다는 (=차이가 없다) 이기 때문에 0 임, 즉 우연일 확률인 95%는 0~95% 까지이고 우연이 아닐 확률인 5%는 95%~100% 까지임
양측 검정
양측 검정은 크거나 작다를 모두 포함한 경우이기 때문에, 유의수준 5%를 두개로 나눠 생각해야한다.
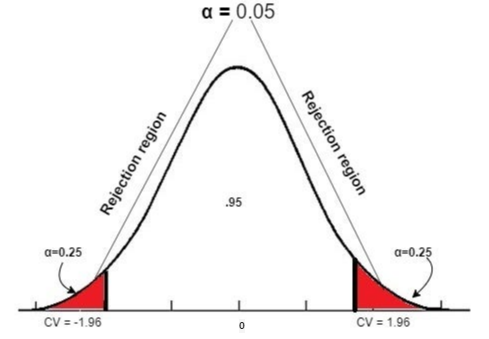
- 따라서, 차이인 1.4cm가 .95 영역 안에서 나오면 우연일 것이다
- 하지만, 차이인 1.4cm가 0.25 영역안 에서 나오면 우연이 아닌 것이다.
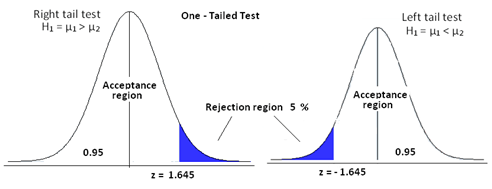
단측 검정
단측 검정은 한쪽 방향만 사용하기 때문에, 유의수준 5%를 그대로 가져간다.
하지만, 크다 / 작다로 결정한 대립가설에 따라 우측검정과 좌측검정으로 나뉜다.
결론
- 양측검정과 단측검정의 차이는 대립가설의 차이에서 발생한다
- 양측은 0 보다 크거나 작은 두 가지를 모두 포함하므로 분포곡선의 양쪽 꼬리 면적의 합이 5%에 들어갈 만큼 크거나 작아야한다
- 단측은 0보다 크다 (우측검정) 와 / 0보다 작다 (좌측검정)의 두가지로 나누어 볼 수 있고 어느 한쪽 꼬리의 면적이 5%에 들어갈 만큼 크거나 작아야한다.
- 0을 기준으로 두 검정에서 95%안에 들어오면 두 평균값의 차이인 Da-b는 우연히 발생한 것이므로 두 집단의 평균값은 통계적으로는 같은 것이다.
다음 강의에서 찐 t-test를 만나뵙겠습니다..
출처
- Sapientia a Dei
t-test (t-검정)이란 무엇인가?
t-test (t-검정)에 대한 동영상 모음
www.youtube.com
