- 머신러닝의 핵심 아이디어는 X와 Y의 관계를 찾는 것인데 주 관심은 Y, 즉 예측하려는 대상에 있다.
- Y를 설명하는 X변수는 보통 여러 개로, X변수들을 수많은 방식 조합하여 Y를 표현할 수 있기에 여러개의 X와 Y의 관계를 찾는 것이다.
- 수학적으로 표현하면, Y = f (X1, X2, X3, ... , Xn) 이다. * 머신러닝에서 함수는 모델이 됨
X와 Y의 관계 찾기
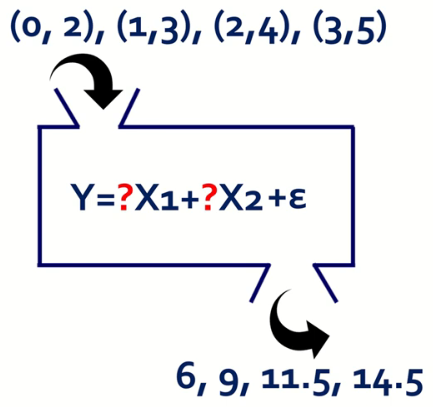
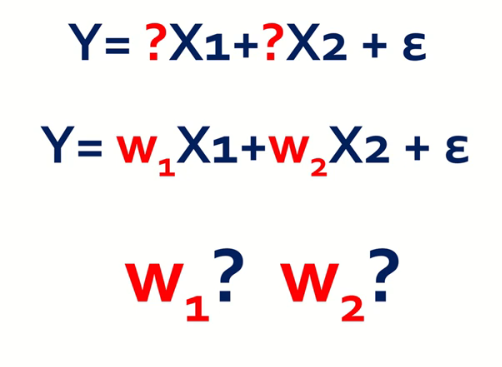
이렇게 X, Y로 함수식을 찾아야하는데, 관계가 복잡해질 수록 함수식을 찾기 어렵기에 X값 앞에 무언가가 붙을 수도 있고, X값만으로 Y값을 찾지 못할 수도 있다.
X값만으로 식을 표현하지 못할 때는 앱실론 ( ε) 을 통해 식을 표현할 수 있다.
Y = ?X1 + ?X2 + ε 를 좀 더 포멀하게 표현하기 위해 Y = w1X1 + w2X2 + ε 이라 썼다했을 때,
과연 ? 값, 즉 w1, w2 값들은 뭘까? 머신러닝에서는 이러한 값을 파라미터라고 부른다.
결국 데이터가 주어졌을 때 모델의 파라미터를 찾는 것이 궁극적인 목적이 된다.
파라미터 추정
Y = w1X1 + w2X2 + ε 에서 X로 표현할 수 있는 부분을 f(X)로 표시해준다면 Y = f(X) + ε이 된다.
이를 ε 기준으로 다시 조합해보면 ε = Y - f(X)가 되는데, 이는 Y값에서 X로 설명할 수 있는 Y값 (= 모델로 부터 나오는 값)을 빼준 값으로, 오차가 된다 (즉, ε = 오차)
따라서, 가장 좋은 모델은 Y - f(X) = 0 으로 ε = 0이 되는 모델이다
ε = Y - f(X) 의 식에서 f(X)는 손실함수라고 칭한다.
- ε = Y - f(X)
- = ε = Y - (w1X1 + w2X2)
- but, 관측치의 개수가 많기 때문에 εi = Yi - (w1X1i + w2X2i), i = 1,2, ...., n *n은 관측치의 개수
- 머신러닝의 핵심 아이디어는 X와 Y의 관계를 찾는 것인데 주 관심은 Y, 즉 예측하려는 대상에 있다.
- Y를 설명하는 X변수는 보통 여러 개로, X변수들을 수많은 방식 조합하여 Y를 표현할 수 있기에 여러개의 X와 Y의 관계를 찾는 것이다.
- 수학적으로 표현하면, Y = f (X1, X2, X3, ... , Xn) 이다. * 머신러닝에서 함수는 모델이 됨
X와 Y의 관계 찾기

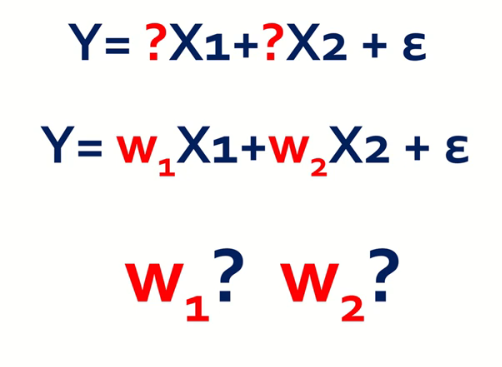
이렇게 X, Y로 함수식을 찾아야하는데, 관계가 복잡해질 수록 함수식을 찾기 어렵기에 X값 앞에 무언가가 붙을 수도 있고, X값만으로 Y값을 찾지 못할 수도 있다.
X값만으로 식을 표현하지 못할 때는 앱실론 ( ε) 을 통해 식을 표현할 수 있다.
Y = ?X1 + ?X2 + ε 를 좀 더 포멀하게 표현하기 위해 Y = w1X1 + w2X2 + ε 이라 썼다했을 때,
과연 ? 값, 즉 w1, w2 값들은 뭘까? 머신러닝에서는 이러한 값을 파라미터라고 부른다.
결국 데이터가 주어졌을 때 모델의 파라미터를 찾는 것이 궁극적인 목적이 된다.
파라미터 추정
Y = w1X1 + w2X2 + ε 에서 X로 표현할 수 있는 부분을 f(X)로 표시해준다면 Y = f(X) + ε이 된다.
이를 ε 기준으로 다시 조합해보면 ε = Y - f(X)가 되는데, 이는 Y값에서 X로 설명할 수 있는 Y값 (= 모델로 부터 나오는 값)을 빼준 값으로, 오차가 된다 (즉, ε = 오차)
따라서, 가장 좋은 모델은 Y - f(X) = 0 으로 ε = 0이 되는 모델이다
ε = Y - f(X) 의 식에서 f(X)는 손실함수라고 칭한다.
- ε = Y - f(X)
- = ε = Y - (w1X1 + w2X2)
- but, 관측치의 개수가 많기 때문에 εi = Yi - (w1X1i + w2X2i), i = 1,2, ...., n *n은 관측치의 개수
